Самоучитель Mathcad Prime 3.0
Первая производная Для того чтобы продифференцировать функцию f (х) в некоторой точке:. Определите точку х, в которой будет вычислена производная, например х:=1. Введите оператор дифференцирования нажатием кнопки Derivative (Производная) на панели Calculus (Вычисления) или введите с клавиатуры вопросительный знак. В появившихся местозаполнителях (рис. 7.3) введите функцию, зависящую от аргумента х, т. F(х), и имя самого аргумента х.
Free mathcad prime 3.0 самоучитель download software at UpdateStar.
Введите оператор численного или символьного вывода для получения ответа. Оператор дифференцирования Пример дифференцирования функции f(x)=cos(x)ln(x) приведен в листинге 7.10.
Mathcad Prime 3.0 Самоучитель
- Описание программы Mathcad Prime 3.0. Mathcad, продукт компании PTC, предназначен для автоматизации.
- Скачать и установить Mathcad Prime 3.0 Русская версия бесплатно. Нажмите по ссылке 'Скачать.
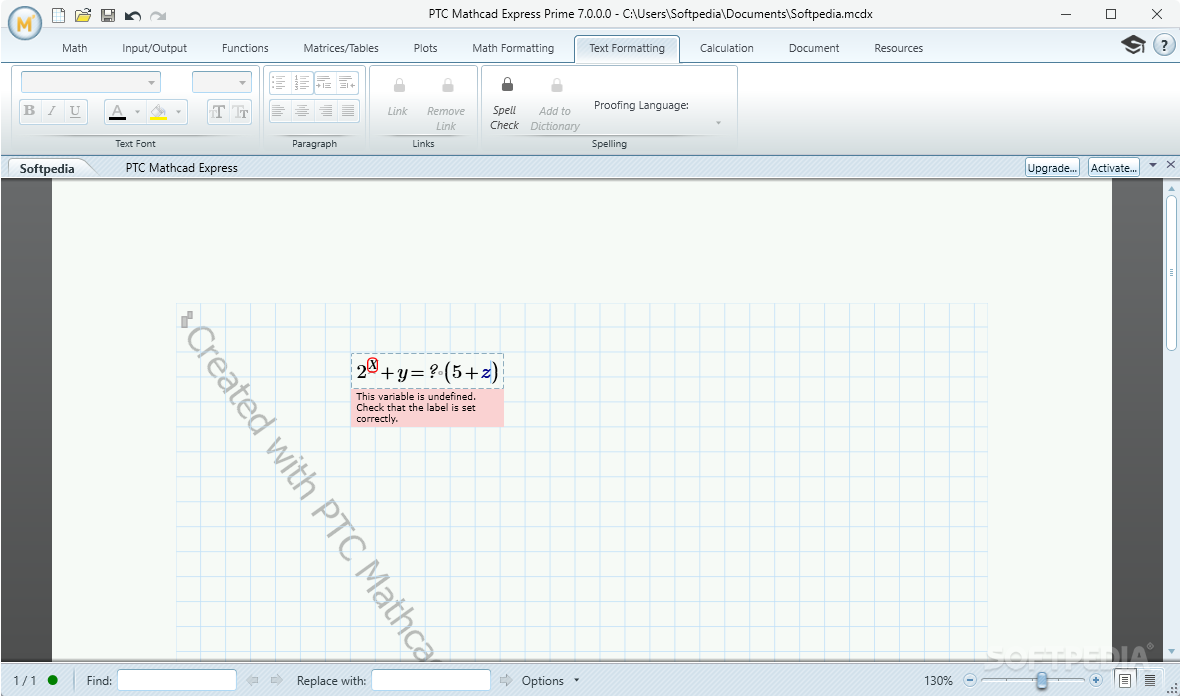
Листинг 7.10. Численное и символьное дифференцирование Не забывайте предварительно определять точку, в которой производится численное дифференцирование, как это сделано в первой строке листинга 7.10. Иначе будет выдано сообщение об ошибке, показанное на рис.
7.4, гласящее, что переменная или функция, входящая в выражение, ранее не определена. Между тем, символьное дифференцирование не требует обязательного явного задания точки дифференцирования В этом случае вместо значения производной (числа или числового выражения) будет выдана аналитическая зависимость (см. Верхнюю часть рис. Ошибка в применении оператора дифференцирования Конечно, можно, как и при использовании других операторов, предварительно определить функцию в отдельном выражении, а затем посчитать ее производную (см. Листинг 7.11); или применить оператор дифференцирования для определения собственных функций пользователя (см.
Листинг 7.12). Листинг 7.11. Символьное и численное дифференцирование функции пользователя Листинг 7.12. Определение функции через оператора дифференцирования В обоих листингах первой строкой определяется функция f (x)=1/x. Во второй строке листинга 7.11 с помощью символьного процессора находится аналитическое выражение ее производной, а в оставшейся части, подобно листингу 7.10, сначала численно, а затем аналитически определяются значения этой производной в точке х=0.1. В листинге 7.12 через производную от f (х) определяется еще одна пользовательская функция д(х) и затем находится ее конкретное значение в той же точке х=0.1. Как Вы заметили, оператор дифференцирования, в основном, соответствует его общепринятому математическому обозначению.
Подключение автоматики. Насоса «ДЖИЛЕКС. Блок автоматики. Главная / насосы ДЖИЛЕКС / Блок автоматики. Блок автоматики может. 
Учебник По Mathcad Prime 3.0
Однако в некоторых случаях при его вводе следует проявить осторожность. Рассмотрим один показательный пример, приведенный в листинге 7.13. Его первые две строки вычисляют производную sin(x) в точке х=0.5. Последняя строка демонстрирует неправильное применение оператора дифференцирования. Вместо вычисления производной sin(x) в той же точке, как этого можно было ожидать, получено нулевое значение.
Это случилось потому, что аргумент функции sin(x) введен не в виде переменной х, а в виде числа. Поэтому Mathcad воспринимает последнюю строку как вычисление сначала значения синуса в точке х=0.5, а затем дифференцирование этого значения (т. Константы) также в точке х=0.5, в соответствии с требованием первой строки листинга.
Поэтому ответ, на самом деле, неудивителен — в какой точке ни дифференцируй константу, результатом будет ноль. Листинг 7.1З. Приер правильного и неправильного применения дифференцирования Для численного дифференцирования Mathcad применяет довольно сложный алгоритм, вычисляющий производную с колоссальной точностью до 7-8-го знака после запятой. Vsti spectrasonics atmosphere для windows 7 torrent. Этот алгоритм (метод Риддера) описан во встроенной справочной системе Mathcad, доступной через меню Help (Справка). Погрешность дифференцирования не зависит от констант TOL или CTOL, в противоположность большинству остальных численных методов, а определяется непосредственно алгоритмом.

Исключение составляют функции, которые дифференцируются в окрестности сингулярной точки; например для рассмотренной нами функции f (x)=1/x это будут точки вблизи х=о. При попытке найти ее производную при х=о будет выдано сообщение об одной из ошибок деления на ноль 'Can't divide by zero' (Деление на ноль невозможно) или 'Found a singularity while evaluating this expression. You may be dividing by zero' (Найдена сингулярность при вычислении этого выражения. Возможно, Вы делите на ноль). Если попробовать численно определить производную очень близко к нулю, например, при х=10 -100, то может появиться сообщение об ошибке 'Can't converge to a solution' (Невозможно найти решение). Встретившись с одной из упомянутых ошибок, присмотритесь повнимательнее к дифференцируемой функции и убедитесь, что Вы не имеете дело с точкой сингулярности.